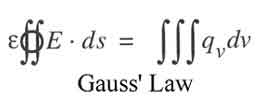Gauss' Law
The third of Maxwell’s four equations is Gauss’ Law, named after the German physicist Carl Friedrich Gauss. Gauss’ Law says that electric charge, qv, (i.e., static electricity) generates an electric field, E (voltage).
This equation says that if you want more electric field, just get more charge. You can get more charge by using things like a Van de Graaff generator (a type of electrostatic generator), or by simply shuffling your feet along a rug on a dry day. If you get too much charge, Gauss’ Law says you get too much electric field. Too much electric field means too much voltage. An excess of voltage creates arcs and sparks.
The left hand side (that is, left of the equal sign) of Gauss’ Law says to add up all the electric field passing through a closed surface, like a sphere [note the little circle on the two integral signs (the S-like symbols)]. A surface like a disk or a bowl is not a closed surface. Gauss’ Law works only with a closed surface like a sphere.
The right hand side, with the three integration symbols, says to add up all the charge, or static electricity, inside that same sphere, or closed surface, that we used for the left hand side of the equation. If you have more charge inside the sphere, you have more electric field (or voltage) crossing the surface of the sphere.
The very first symbol (ε) in Gauss’ Law is the Greek letter e, epsilon. This is also called a dielectric constant. Good insulators, like ceramic and glass, can have a large dielectric constant. Since the dielectric constant multiplies the left hand side, the effect of a large dielectric constant is to decrease the electric field, and thus the voltage, required for a given amount of charge. Electronic components called capacitors store charge. If you want to store more charge for a given voltage, Gauss’ Law tells us to just add something like glass, which has a high dielectric constant.
Gauss’ Law was inspired by Coulomb’s Law, which states that the force between two charged spheres is inversely proportional to the square of the distance between them.